De gulden snede wordt vaak genoemd als de maatstaf voor schoonheid, of het nu gaat om kunst, architectuur of zelfs de mens. Maar klopt dit eigenlijk wel?
Wat is de gulden snede?
De gulden snede is een wiskundige verhouding die vaak in de natuur zou voorkomen. De verhouding komt neer op het getal 1,618 en wordt in wiskundige middens aangeduid met de Griekse letter phi. Sommigen beweren zelfs dat het ideale lichaam volledig volgens deze verhouding is opgebouwd. Daarvoor verwijst men vaak naar de Man van Vitruvius – gekend van de wereldberoemde tekening van Leonardo Da Vinci, die ook op onze euromunt staat. Maar eigenlijk klopt dit helemaal niet. Als men echt deze verhouding zou toepassen, dan heeft men een veel grotere cirkel nodig dan op de tekening het geval is.
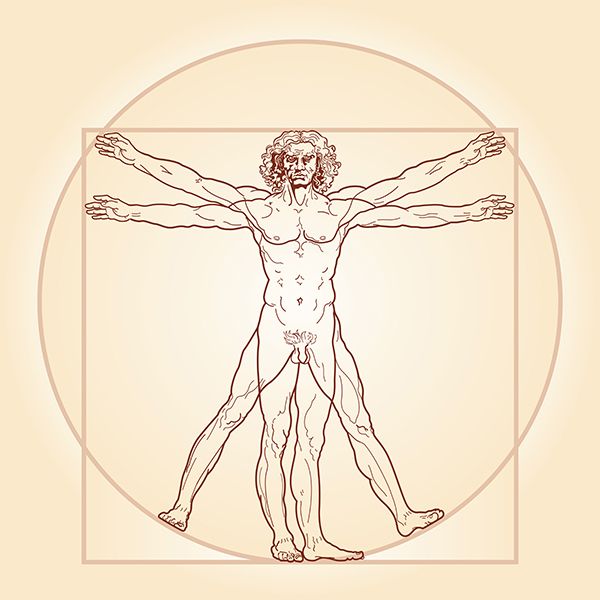
Man van Vitruvius
Wel wordt de gulden snede vaak toegepast in kunst, denk maar aan de schilderijen van de Spaanse surrealist Salvador Dalì of de werken van de vermaarde Zwitserse architect Le Corbusier. Een wereldberoemd voorbeeld van een gebouw waarvan de afmetingen quasi voldoen aan de gulden snede is de grote piramide van Giza.
Waarom vinden we het mooi?
Hoe komt het nu dat we kunst, architectuur of zelfs muziek toegepast volgens de gulden snede zo mooi vinden? Dat zou liggen aan het feit dat het alomtegenwoordig is in de natuur. Aangezien we die verhouding dus gewoon zijn, zouden we kunstwerken, gebouwen, objecten of zelfs mensen van wie de afmetingen eraan voldoen mooi vinden.
Wie zijn de mooiste mensen volgens de gulden snede?
Een Britse chirurg dokterde uit welke beroemde mannen volgens de gulden snede de allerknapste van de aardbol zijn. Volgens Dr. De Silva is George Clooney de absolute nummer 1, gevolgd door Bradley Cooper, Brad Pitt, Harry Styles en David Beckham. De Silva maakte ook een lijstje van de mooiste vrouwen volgens deze verhouding. Daar staat Bella Hadid op de eerste plaats, Beyoncé op nummer 2 en vervolgens Amber Heard, Ariana Grande en Taylor Swift.

Brad Pitt en George Clooney
Een beetje relativering
Of de gulden snede nu werkelijk een maatstaf is voor schoonheid, dat valt natuurlijk zeer sterk te betwijfelen. Zelf geloven we er alvast niet in en we zijn niet de enige. Zo toont het Twitter-account Fibonnaci Perfection aan dat heel wat dingen die wel voldoen aan deze verhouding absoluut arbitrair zijn.
Ignatius Farray (@IgnatiusFarray1) pic.twitter.com/CNLkz3MBze
— Fibonacci Perfection (@FibonacciSpiral) 2 juli 2016

























